A Markov chain can be used to model the evolution of a sequence of random events where probabilities for each depend solely on the previous event. Once a state in the sequence is observed, previous values are no longer relevant for the prediction of future values. Markov chains have many applications for modeling real-world phenomena in a myriad of disciplines including physics, biology, chemistry, queueing, and information theory. More recently, they are being recognized as important tools in the world of artificial intelligence (AI) where algorithms are designed to make intelligent decisions based on context and without human input. Markov chains can be particularly useful for natural language processing and generative AI algorithms where the respective goals are to make predictions and to create new data in the form or, for example, new text or images. In this course, we will explore examples of both. While generative AI models are generally far more complex than Markov chains, the study of the latter provides an important foundation for the former. Additionally, Markov chains provide the basis for a powerful class of so-called Markov chain Monte Carlo (MCMC) algorithms that can be used to sample values from complex probability distributions used in AI and beyond.

Discover new skills with 30% off courses from industry experts. Save now.


Discrete-Time Markov Chains and Monte Carlo Methods
This course is part of Foundations of Probability and Statistics Specialization

Instructor: Jem Corcoran
Included with 
Recommended experience
What you'll learn
Analyze long-term behavior of Markov processes for the purposes of both prediction and understanding equilibrium in dynamic stochastic systems
Apply Markov decision processes to solve problems involving uncertainty and sequential decision-making
Simulate data from complex probability distributions using Markov chain Monte Carlo algorithms
Skills you'll gain
Details to know

Add to your LinkedIn profile
August 2025
15 assignments
See how employees at top companies are mastering in-demand skills

Build your subject-matter expertise
- Learn new concepts from industry experts
- Gain a foundational understanding of a subject or tool
- Develop job-relevant skills with hands-on projects
- Earn a shareable career certificate

There are 6 modules in this course
Welcome to the course! This module contains logistical information to get you started!
What's included
7 readings4 ungraded labs
In this module we will review definitions and basic computations of conditional probabilities. We will then define a Markov chain and its associated transition probability matrix and learn how to do many basic calculations. We will then tackle more advanced calculations involving absorbing states and techniques for putting a longer history into a Markov framework!
What's included
12 videos5 assignments2 programming assignments
What happens if you run a Markov chain out for a "very long time"? In many cases, it turns out that the chain will settle into a sort of "equilibrium" or "limiting distribution" where you will find it in various states with various fixed probabilities. In this Module, we will define communication classes, recurrence, and periodicity properties for Markov chains with the ultimate goal of being able to answer existence and uniqueness questions about limiting distributions!
What's included
9 videos3 assignments2 programming assignments
In this Module, we will define what is meant by a "stationary" distribution for a Markov chain. You will learn how it relates to the limiting distribution discussed in the previous Module. You will also spend time learning about the very powerful "first-step analysis" technique for solving many, otherwise intractable, problems of interest surrounding Markov chains. We will discuss rates of convergence for a Markov chain to settle into its "stationary mode", and just maybe we'll give a monkey a keyboard and hope for the best!
What's included
11 videos3 assignments2 programming assignments
In this Module we explore several options for simulating values from discrete and continuous distributions. Several of the algorithms we consider will involve creating a Markov chain with a stationary or limiting distribution that is equivalent to the "target" distribution of interest. This Module includes the inverse cdf method, the accept-reject algorithm, the Metropolis-Hastings algorithm, the Gibbs sampler, and a brief introduction to "perfect sampling".
What's included
13 videos2 assignments2 programming assignments4 ungraded labs
In reinforcement learning, an "agent" learns to make decisions in an environment through receiving rewards or punishments for taking various actions. A Markov decision process (MDP) is reinforcement learning where, given the current state of the environment and the agent's current action, past states and actions used to get the agent to that point are irrelevant. In this Module, we learn about the famous "Bellman equation", which is used to recursively assign rewards to various states and how to use it in order to find an optimal strategy for the agent!
What's included
5 videos2 assignments2 programming assignments4 ungraded labs
Earn a career certificate
Add this credential to your LinkedIn profile, resume, or CV. Share it on social media and in your performance review.
Instructor

Offered by
Explore more from Probability and Statistics

University of Colorado Boulder
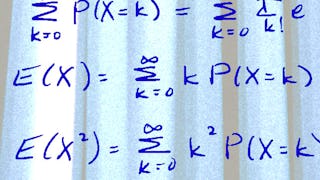
University of Colorado Boulder
Why people choose Coursera for their career





Open new doors with Coursera Plus
Unlimited access to 10,000+ world-class courses, hands-on projects, and job-ready certificate programs - all included in your subscription
Advance your career with an online degree
Earn a degree from world-class universities - 100% online
Join over 3,400 global companies that choose Coursera for Business
Upskill your employees to excel in the digital economy
Frequently asked questions
Yes, you can preview the first video and view the syllabus before you enroll. You must purchase the course to access content not included in the preview.
If you decide to enroll in the course before the session start date, you will have access to all of the lecture videos and readings for the course. You’ll be able to submit assignments once the session starts.
Once you enroll and your session begins, you will have access to all videos and other resources, including reading items and the course discussion forum. You’ll be able to view and submit practice assessments, and complete required graded assignments to earn a grade and a Course Certificate.
More questions
Financial aid available,